Solution to Abstract Algebra by Dummit & Foote 3rd edition Chapter 3.2 Exercise 3.2.13
Fix any labeling of the vertices of a square and use this to identify $D_8$ as a subgroup of $S_4$. Prove that the subgroups $D_8$ and $\langle (1\ 2\ 3) \rangle$ do not commute in $S_4$.
Solution: We can label the vertices of a square as follows.
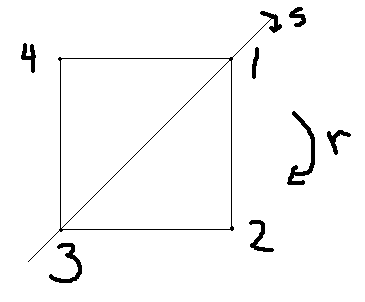
Now a 90 degree clockwise rotation corresponds to the permutation $(1\ 2\ 3\ 4)$ and a reflection across the $(1\ 3)$ axis to $(2\ 4)$.
Now let $$H = \langle (1\ 2\ 3\ 4), (2\ 4) \rangle$$ and $$K = \langle (1\ 2\ 3) \rangle.$$ If $HK = KH$, then in particular $$(1\ 2\ 3\ 4)(1\ 2\ 3)(1\ 4\ 3\ 2) = (2\ 3\ 4) \in K,$$ a contradiction. So $HK \neq KH$.