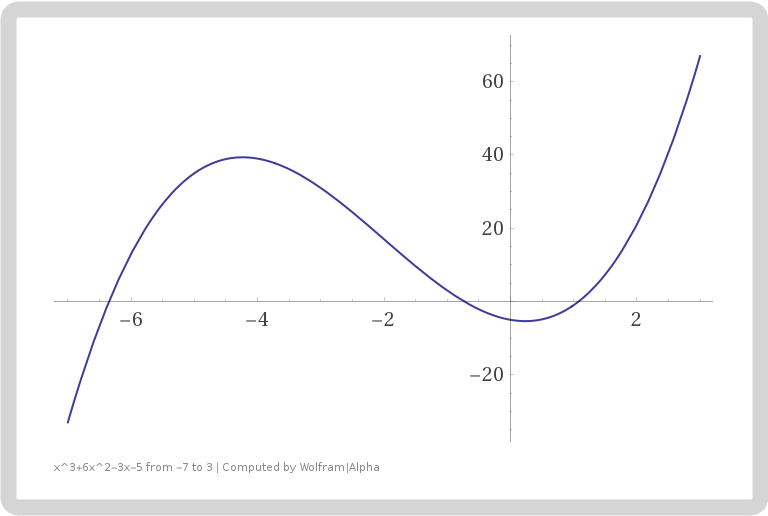
Consider the univariate function $$f(x)=x^3+6x^2-3x-5.$$Find its stationary points and indicate whether they are maximum, minimum, or saddle points.
I will assume you are familiar with Calculus, see the book Calculus for more details.
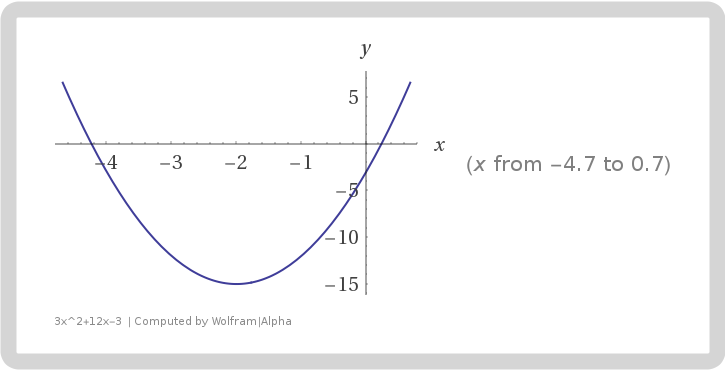
Solution: First, we compute the derivative of $f(x)$, $$f'(x)=3x^2+12x-3=3(x^2+4x-1).$$Its stationary points (also known as critical points) are the zeros of derivative. Hence by quadratic formula, we see that the stationary points are $$x_1=-2+\sqrt{5},\quad x_2=-2-\sqrt{5}.$$To determine the local extreme values, we have find the signs of the derivative on some intervals. Since we know that the graph of the derivative is an open-upward parabola with $x$-intercepts $-2\pm \sqrt 5$, it is clear that the function $f'(x)$ is positive on $(-\infty,-2-\sqrt 5)$ and $(-2+\sqrt 5,\infty)$ and negative on $(-2-\sqrt 5,-2+\sqrt 5)$. Below is the graph of the derivative.
Hence by the first derivative test, we see that the original function has local maximum at $x_2=-2-\sqrt{5}$ and local minimum at $x=-2+\sqrt{5}$. There is no global maximum or global minimum since $f(-\infty)=-\infty$ and $f(\infty)=\infty$. Here is the graph of the original function.