Consider whether the following statements are true or false:
(a) The intersection of any two convex sets is convex.
Solution: True. Let $\mathcal C_1$ and $\mathcal C_2$ be two convex sets. We would like to show that $\mathcal C_1\cap \mathcal C_2$ is convex.
If $\mathcal C_1\cap \mathcal C_2$ is empty then we are done. Suppose $\mathcal C_1\cap \mathcal C_2$ is nonempty. By definition 7.2, we would like to show that for any $x, y\in \mathcal C_1\cap \mathcal C_2$, we have $$\theta x +(1-\theta)y\in \mathcal C_1\cap \mathcal C_2$$for all $\theta\in [0,1]$.
Since $x, y\in \mathcal C_1\cap \mathcal C_2$, we have $x, y\in \mathcal C_1$. By definition 7.2 we have \begin{equation}\label{mml7.3.1}\theta x +(1-\theta)y\in \mathcal C_1\end{equation}for all $\theta\in [0,1]$. Similarly, we have \begin{equation}\label{mml7.3.2}\theta x +(1-\theta)y\in \mathcal C_2\end{equation}for all $\theta\in [0,1]$. Therefore, combining \eqref{mml7.3.1} and \eqref{mml7.3.2}, we have$$\theta x +(1-\theta)y\in \mathcal C_1\cap \mathcal C_2$$for all $\theta\in [0,1]$. Hence the statement is true.
Remark: The intersection of any convex sets (not necessarily finitely many) is convex.
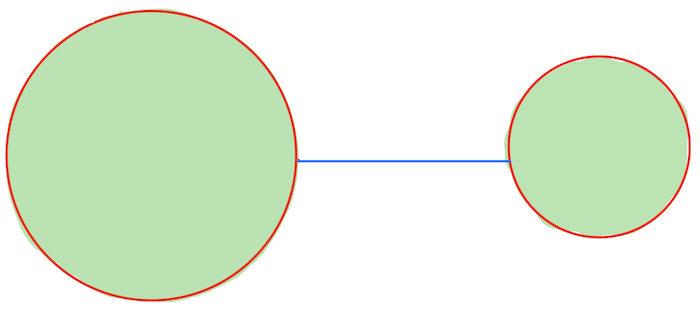
(b) The union of any two convex sets is convex.
Solution: False. Definition 7.2 can be restated as follows: A set is convex if and only if the segment connecting any two points in this set is again contained in this set. Here is a counterexample. Take two disks which are non-intersecting. Clearly, a disk is convex. But they are union is not. Because the blue segment is not contained in the union of the two disks.
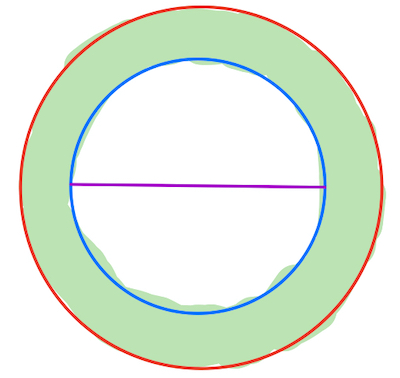
(c) The difference of a convex set $A$ from another convex set $B$ is convex.
Solution: False. Take a big disk and removing a smaller disk inside of it. See the picture below. Then the new set shaded in green color is not convex because the purple segment is not contained in the new set.