Solution to Abstract Algebra by Dummit & Foote 3rd edition Chapter 1.4 Exercise 1.4.11
Let $F$ be a field, and define the Heisenberg group $H(F)$ over, $F$ by
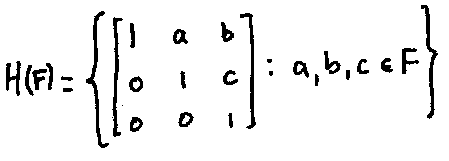
(1) Show that $H(F)$ is closed under matrix multiplication. Demonstrate explicitly that $H(F)$ is always non-abelian.
(2) Given $X \in H(F)$, find an explicit formula for $X^{-1}$ and deduce that $H(F)$ is closed under inversion.
(3) Prove the associative law for $H(F)$ under matrix multiplication. Deduce that $H(F)$ is a group.
(4) Find the order of each element of the finite group $H(\mathbb{F}_2)$.
(5) Prove that every nonidentity element of the group $H(\mathbb{R})$ has infinite order.
Solution:
(1) Let $X, Y \in H(F)$, with
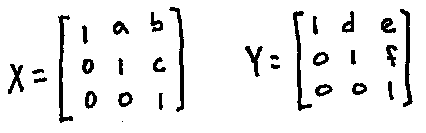
Note that
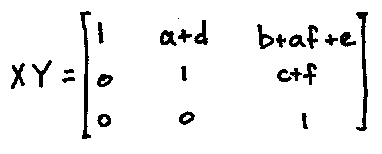
so that $XY \in H(F)$. Thus $H(F)$ is closed under matrix multiplication. Now since $F$ is a field, we always have $0,1 \in F$. Then we have $A, B \in H(F)$, where
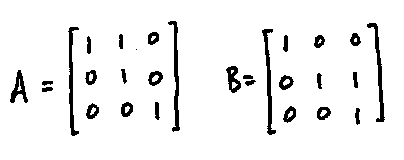
But note that
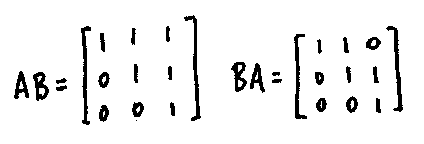
So that $H(F)$ is nonabelian for all $F$ (provided $0 \neq 1$).
(2) We have
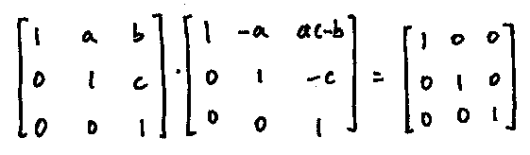
so that
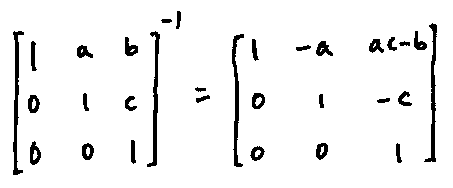
Hence $H(F)$ is closed under matrix inversion.
(3) Note that
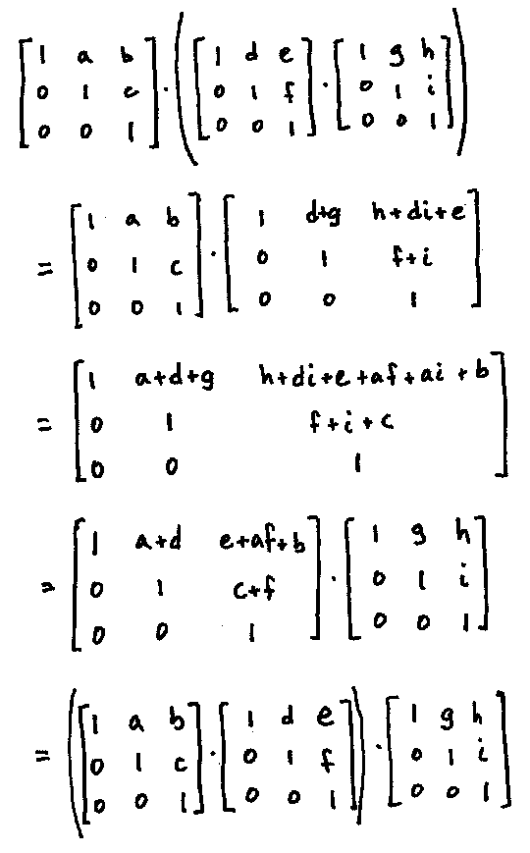
so that matrix multiplication is associative on $H(F)$. Thus $H(F)$ is a group under matrix multiplication; moreover, it is clear that $|H(F)| = |F|^3$.
(4) We will denote the elements of $H(\mathbb{F}_2) by
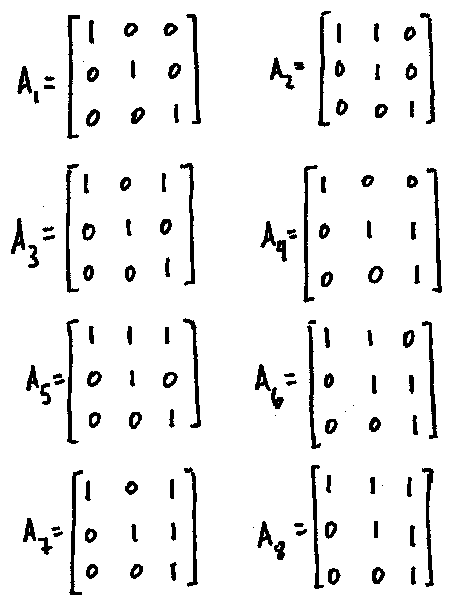
Now $A_2^2 = A_3^2 = A_4^2 = A_5^2 = A_7^2 = I$, so these elements have order 2. Since
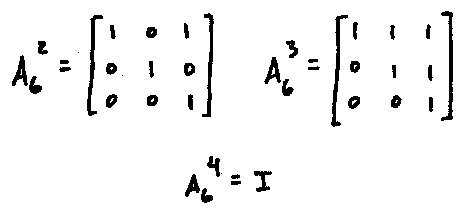
we have that $|A_6| = 4$, and likewise since
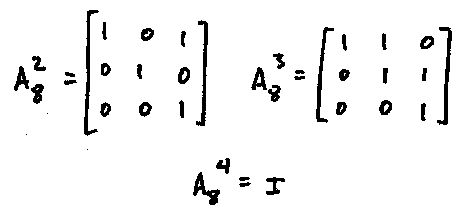
we have $|A_8| = 4$.
(5) We claim that for all $a,b,c \in \mathbb{R}$ and integers $n \geq 1$,
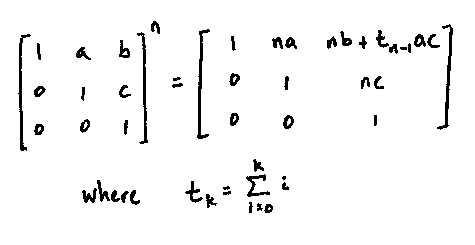
which we prove by induction on $n$. For the base case, we have
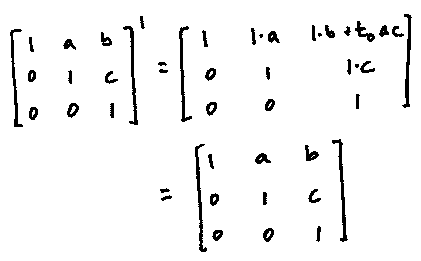
Now suppose the statement holds for $n$. Then
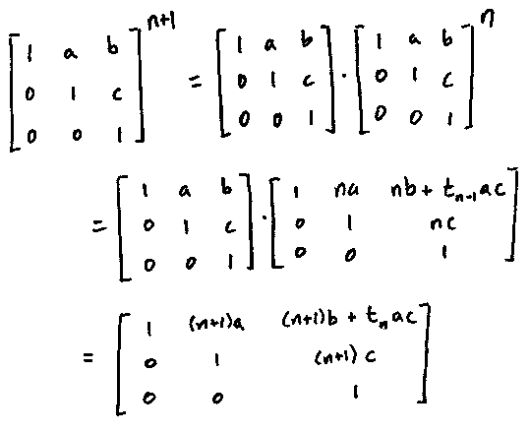
so that it holds also for $n+1$. Thus the statement is proved.
Now consider an arbitrary nonidentity element $X \in H(\mathbb{R})$, where $X$ is defined as above. If either $a$ or $c$ is nonzero, then the (1,2) or the (2,3) element of $X^n$ is nonzero for all positive $n$. If $a = c = 0$, then we have $b \neq 0$ and so the (1,3) entry of $X^n$ is nonzero for all positive $n$.