Solution to Abstract Algebra by Dummit & Foote 3rd edition Chapter 2.3 Exercise 2.3.1
Find all subgroups of $G = \mathbb{Z}/(45)$, giving a generator for each. Describe the containments among these subgroups.
Solution: The subgroups of $G$ correspond bijectively to the positive divisors of $45$ – in particular, if $m$ divides $45$, then $G$ has a subgroup of order $n/m$ given by $\langle m \rangle$, and every subgroup has this form.
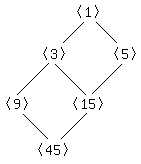
The prime factorization of $45$ is $45 = 3 \cdot 3 \cdot 5$, so that the positive divisors of $45$ are 1, 3, 5, 9, 15, 45. The corresponding subgroups are $\langle 1 \rangle$, $\langle 3\rangle$, $\langle 5 \rangle$, $\langle 9 \rangle$, $\langle 15 \rangle$, and $\langle 45 \rangle$.
We also have that $\langle a \rangle \leq \langle b \rangle$ precisely when $b|a$. We can visualize these containments as in the following diagram; each subgroup is contained in those above it to which it is connected by a line, and we do not draw lines if there is an intermediate subgroup.