Solution to Abstract Algebra by Dummit & Foote 3rd edition Chapter 3.3 Exercise 3.3.5
Let $QD_{16} = \langle \sigma, \tau \rangle$ be the quasidihedral group of order 16 described in Exercise 3.1.18. Prove that $\langle \sigma^4 \rangle$ is normal in $QD_{16}$ and use the Lattice Isomorphism Theorem to draw the lattice of subgroups of $QD_{16}/\langle \sigma^4 \rangle$. Which group of order 8 has the same subgroup lattice? Use generators and relations to determine the isomorphism type of $QD_{16}/\langle \sigma^4 \rangle$.
Solution: Note that $\sigma \sigma^4 \sigma^{-1} = \sigma^4 \in \langle \sigma^4 \rangle$ and $$\tau \sigma^4 \tau^{-1} = \tau \sigma^3 \sigma \tau = \sigma \tau \tau \sigma^3 = \sigma^4 \in \langle \sigma^4 \rangle.$$ By a previous exercise, then, $\langle \sigma^4 \rangle$ is normal in $QD_{16}$.
The subgroup lattice of $QD_{16}/\langle \sigma^4 \rangle$ is as follows.
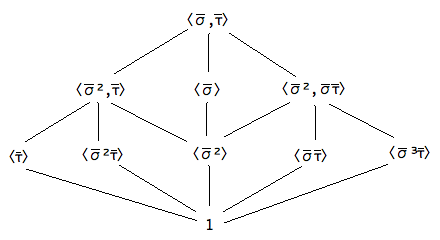
The dihedral group $D_8$ has the same subgroup lattice. Moreover, we have $$QD_{16}/\langle \sigma^4 \rangle = \langle \overline{\sigma}, \overline{\tau} \ |\ \overline{\sigma}^4 = \overline{\tau}^2 = 1, \overline{\sigma} \overline{\tau} = \overline{\tau} \overline{\sigma}^{-1} \rangle,$$ so that $QD_{16}/\langle \sigma^4 \rangle \cong D_8$.