Solution to Abstract Algebra by Dummit & Foote 3rd edition Chapter 3.2 Exercise 3.2.2
Find the lattice of subgroups of $S_3$.
Solution: Every (nontrivial) $\subseteq$-minimal subgroup of $S_3$ is cyclic – i.e., generated by a single nonidentity element. There are 5 such subgroups: $\langle (1\ 2) \rangle$, $\langle (1\ 3) \rangle$, $\langle (2\ 3) \rangle$, $\langle (1\ 2\ 3) \rangle$, and $\langle (1\ 3\ 2) \rangle$. Note that $\langle (1\ 2\ 3) \rangle = \langle (1\ 3\ 2) \rangle$ since $(1\ 2\ 3)^{-1} = (1\ 3\ 2)$.
Moreover, $\langle (1\ 2\ 3) \rangle$ has order 3 and is thus distinct from the other cyclic subgroups, which have order 2. Finally, the order 2 cyclic subgroups are distinct because their generators are distinct. No order 2 subgroup is contained in $\langle (1\ 2\ 3) \rangle$ by Lagrange’s Theorem, so that the distinct nontrivial $\subseteq$-minimal subgroups of $S_3$ are $\langle (1\ 2) \rangle$, $\langle (1\ 3) \rangle$, $\langle (2\ 3) \rangle$, and $\langle (1\ 2\ 3) \rangle$. Clearly any pairwise meet of these subgroups is trivial.
Now every other subgroup of $S_3$ is a finite join of some nontrivial $\subseteq$-minimal subgroups. Let $H$ and $K$ be two such subgroups.
If $|H| = 2$ and $|K| = 3$, then $\mathsf{lcm}(2,3) = 6$ must divide $|\langle H, K \rangle|$ by Lagrange’s Theorem; thus, since $S_3$ is finite, $\langle H,K \rangle = S_3$.
If $|H| = |K| = 2$, then $\mathsf{lcm}(2,2) = 2$ must divide $|\langle H,K \rangle|$ by Lagrange’s Theorem.
If $|\langle H,K \rangle| = 2$, then $\langle H,K \rangle$ has no proper subgroups and thus is $\subseteq$-minimal; that is, $\langle H,K \rangle$ is one of the order 2 subgroups accounted for above, and thus $H = K$.
If $|\langle H,K \rangle| = 4$, we have a contradiction by Lagrange’s Theorem.
If $|\langle H,K \rangle| = 6$, then since $S_3$ is finite we have $\langle H,K \rangle = S_3$.
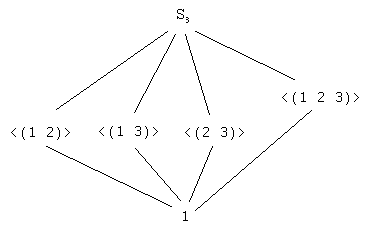
We have seen that the pairwise join of two distinct $\subseteq$-minimal subgroups of $S_3$ is all of $S_3$. Thus, the complete list of subgroups of $S_3$ is as follows: 1, $\langle (1\ 2) \rangle$, $\langle (1\ 3) \rangle$, $\langle (2\ 3) \rangle$, $\langle (1\ 2\ 3) \rangle$, and $S_3$.
Finally, the subgroup lattice of $S_3$ is as follows.