Solution to Abstract Algebra by Dummit & Foote 3rd edition Chapter 3.2 Exercise 3.2.3
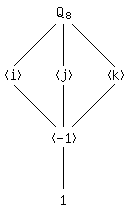
Compute the lattice of subgroups of $Q_8$.
Solution: Every $\subseteq$-minimal subgroup of $Q_8$ is cyclic; disregarding inverses and the identity, there are at most 4 distinct cyclic subgroups of $Q_8$: $\langle -1 \rangle$, $\langle i \rangle$, $\langle j \rangle$, and $\langle k \rangle$. Note that $i^2 = j^2 = k^2 = -1$, so that $\langle -1 \rangle$ is a subgroup of the other three; by Lagrange’s Theorem, there are no intermediate subgroups. Thus $\langle -1 \rangle$ is the only $\subseteq$-minimal subgroup of $Q_8$.
Now by Lagrange’s Theorem, any subgroup of $Q_8$ must have order 1, 2, 4, or 8. A subgroup of order 1 is trivial and a subgroup of order 2 is cyclic. If $H \leq Q_8$ is minimally generated by 2 elements, then those elements are (without loss of generality) $(i,j)$, $(i,k)$, or $(j,k)$. In any case we have $H = Q_8$. We remark that any subgroup minimally generated by $n > 2$ elements contains $Q_8$ as a subgroup and hence is all of $Q_8$. Thus the only order 4 subgroups are cyclic, and we enumerated these above. Lastly, $Q_8$ itself is the only order 8 subgroup.
Thus the subgroup lattice of $Q_8$ is as follows.